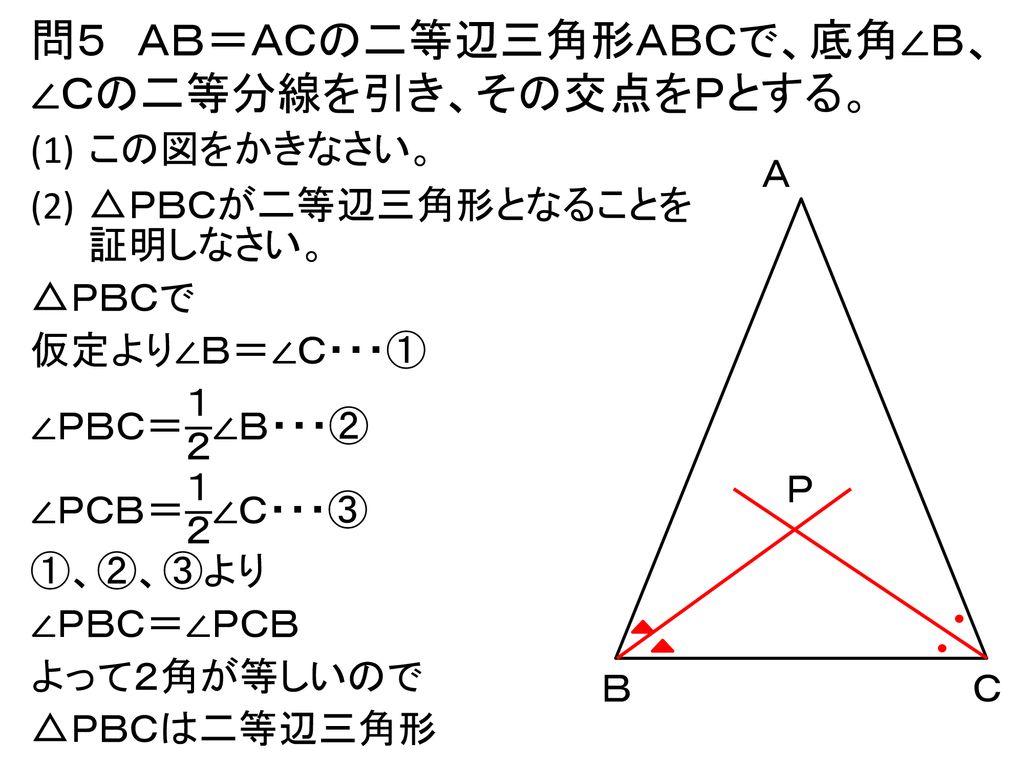
本時のねらい 二等辺三角形の作図から証明を使って性質を導くことができる 定義や定理の用語の意味を理解する Ppt Download
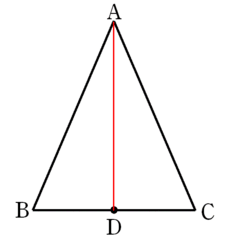
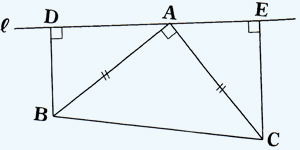
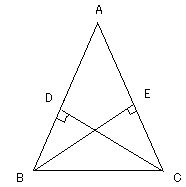
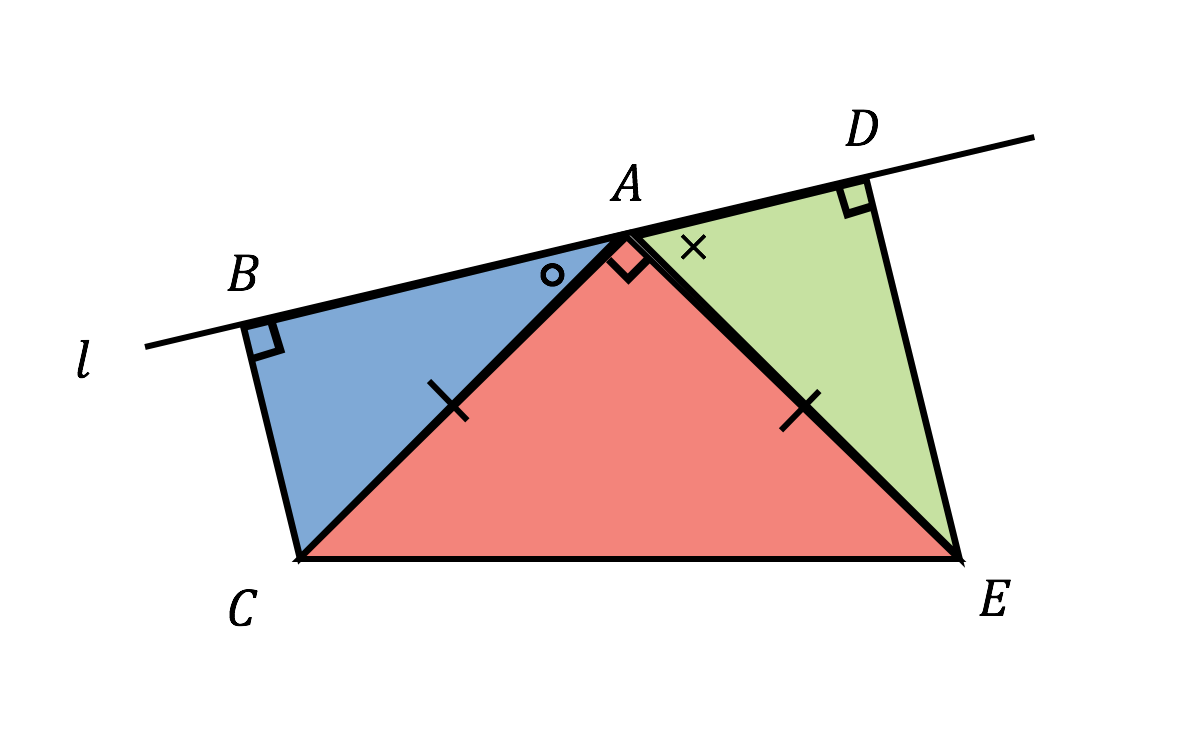
二等辺三角形の底辺の中点 三角形 ABC は、 $\mathrm{ AB }=\mathrm{ AC }$ の二等辺三角形とします。 また、 BC の中点を点 D とします。 このとき、 AD と BC は垂直に交わります。 図形的に考えても、これを示すのはそれほど難しくはありません。三角形証明 (発展1) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 ADEはAD=AE,∠DAE=90°の直角二等辺三角形である。 このときBD=CEを証明しなさい。 次の図のような ABCがある。 辺AC上に点Dがあり、BCの延長上にEがある。 点Dを通り辺BCに平行な直線をnと
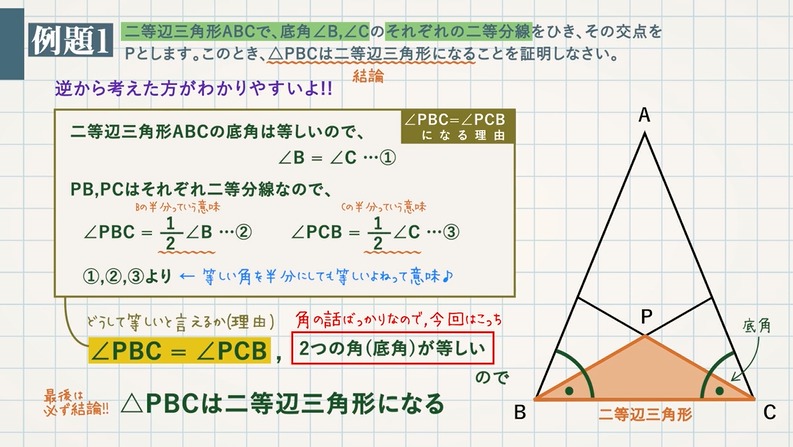
二等辺三角形の証明問題
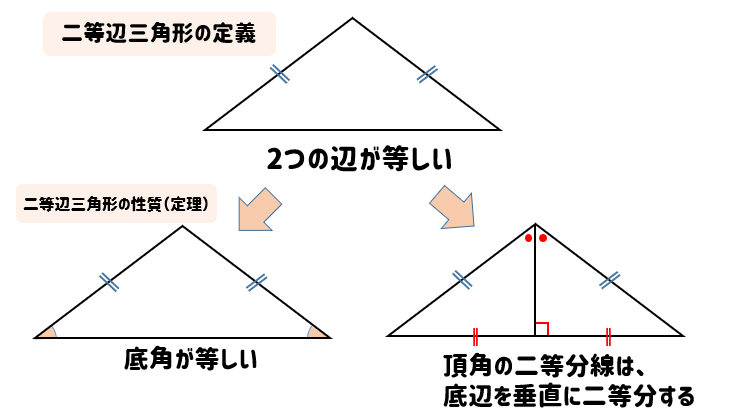
二等辺三角形の証明問題- 二等辺三角形の定義、定理、基本的な証明問題の練習プリントです。定期テストにもよく出題されますので、確実に出来るようにしましょう。 二等辺三角形の定義「二つの辺の長さが等しい三角形」 等しい二辺の間の角を頂角という。 頂角に向い合う辺を底辺という。二等辺三角形の角度、辺の長さとの関係、証明 二等辺三角形の角度で、なぜ低角が等しくなるか考えましょう。二等辺三角形とは、下図のように2辺が等しい三角形です。 形 上図の二等辺三角形の頂角から底辺に向かって垂線を引きます。
Kelas 8 Catatan Tentang 二等辺三角形の性質 Clearnote
二等辺三角形がある」問題です PABが二等辺三角形なので ∠ P B A = ∠ P A B ＝ x ですね ABPの外角に注目して ∠ B P C = ∠ P B A ＋ ∠ B A P ＋ ＝ = x ＋ x ＝ 2 x ABCは二等辺三角形なので ∠ A B C = ∠ A C B ＝ 2 x です ABCの内角の和で方程式を立てて 21年2月19日 この記事では、「合同」とは何か、三角形の合同条件や証明問題について解説していきます。 二等辺三角形や直角三角形の合同条件も説明していくので、ぜひマスターしてくださいね！ 目次 非表示 合同とは？ 合同の記号 合同の性質 頂角を二等分し二辺挟む角相等 2底辺を二等分し三辺相等 3頂角から底辺に垂線を引き直角三角形の斜線と他の一辺相等 をやるはずです しかしこれら3つは証明すべきもの、「二等辺三角形の両底角は等しい」を前提にしてを用いた証明です あきらか循環
右図のように、長方形の用紙を用意し、対角線を折り目にして折ると、重なった部分 FACは二等辺三角形となる。 このことを証明しなさい。 ＜前：『 第4章 図形の調べ方 』 の復習テスト の問題 L34 二等辺三角形（1） の解答：次＞三角形と四角形 問題 z 二等辺三角形 z 二等辺三角形の性質 z 二等辺三角形であるための条件 z 正三角形 z 直角三角形の合同 z 直角三角形の合同条件を使った証明 z 平行四辺形 z 平行四辺形の性質 z 平行四辺形であるための条件 z いろいろな平行四辺直角二等辺三角形の特徴は、 ・辺の長さの比が「1：1：√2」 ・角度が45度 である点です。 上記は是非覚えてください。 下記も参考になります。 直角二等辺三角形と三平方の定理の関係は？ 3分でわかる計算、公式、辺の比、例題
二等辺三角形の証明問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |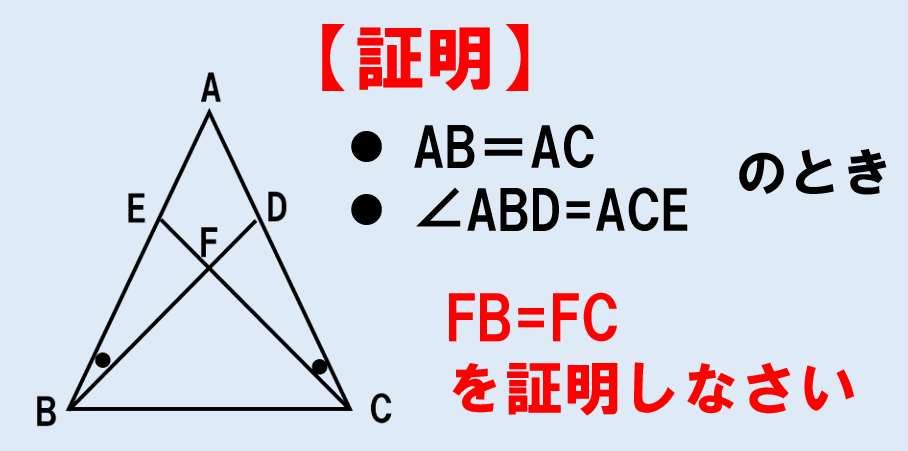
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 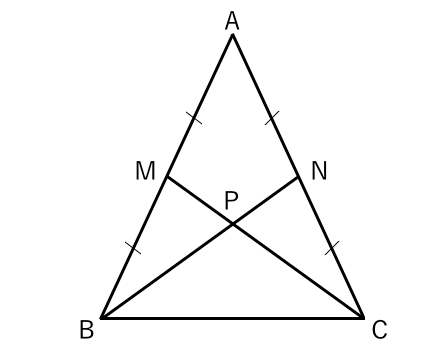Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 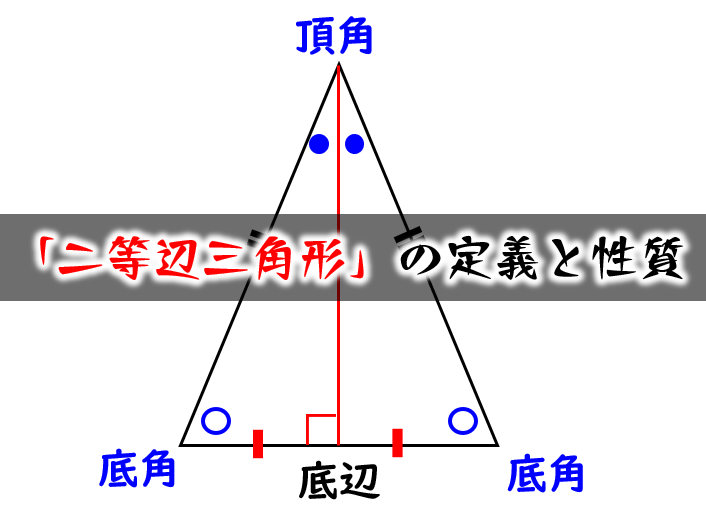 Ed City Daito Osaka Jp |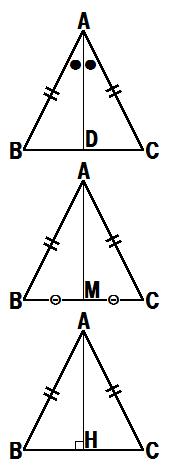
Ed City Daito Osaka Jp | Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 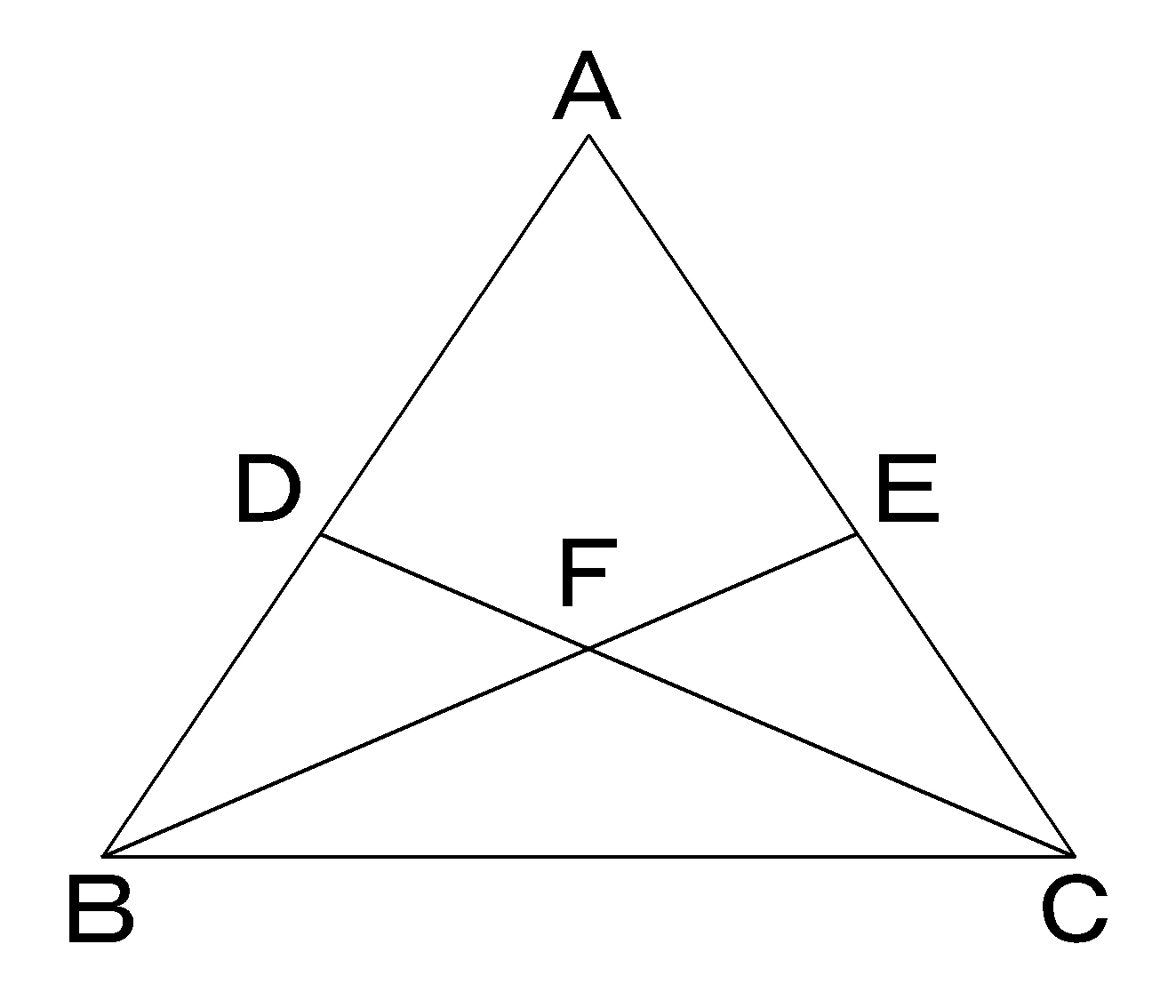Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp | Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |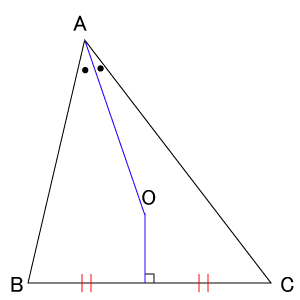
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 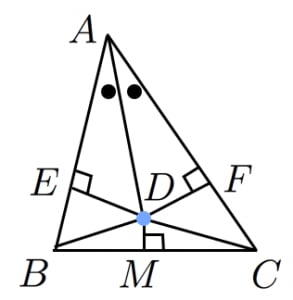 Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 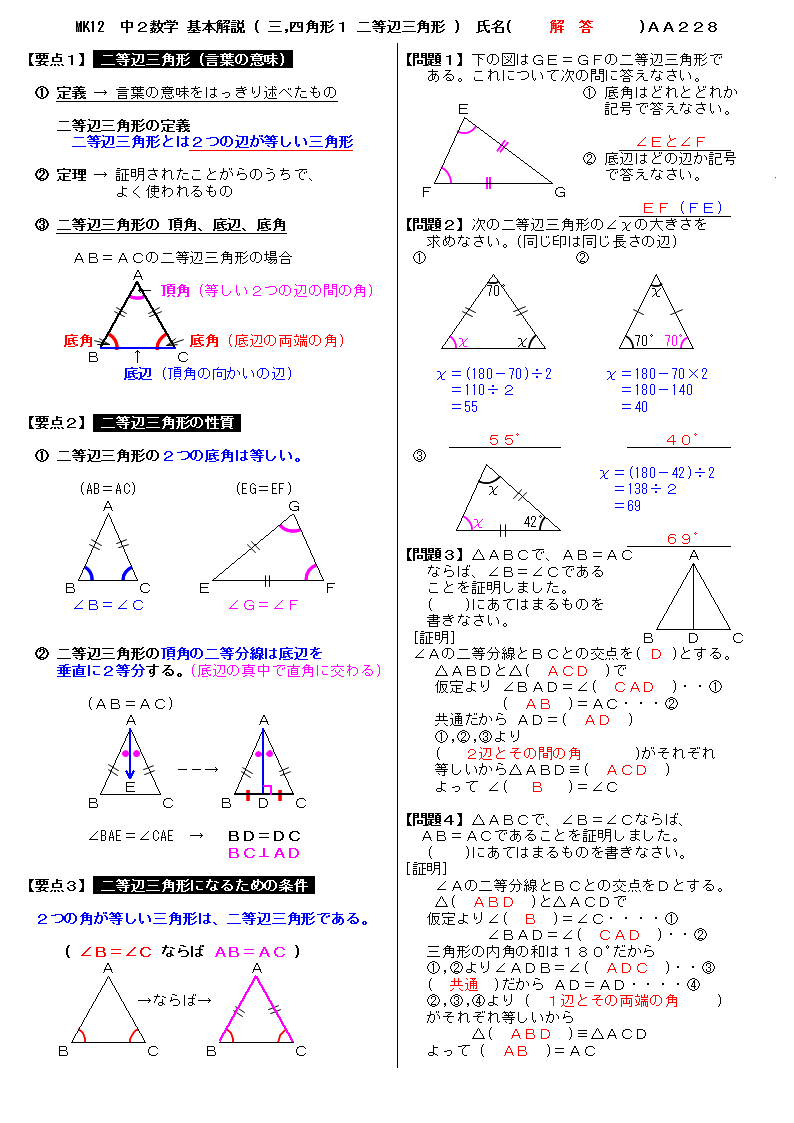 Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 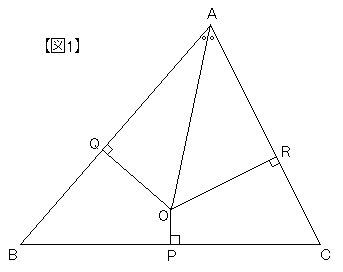Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp | Ed City Daito Osaka Jp | 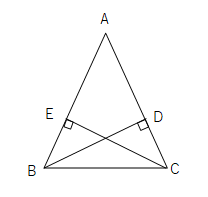 Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |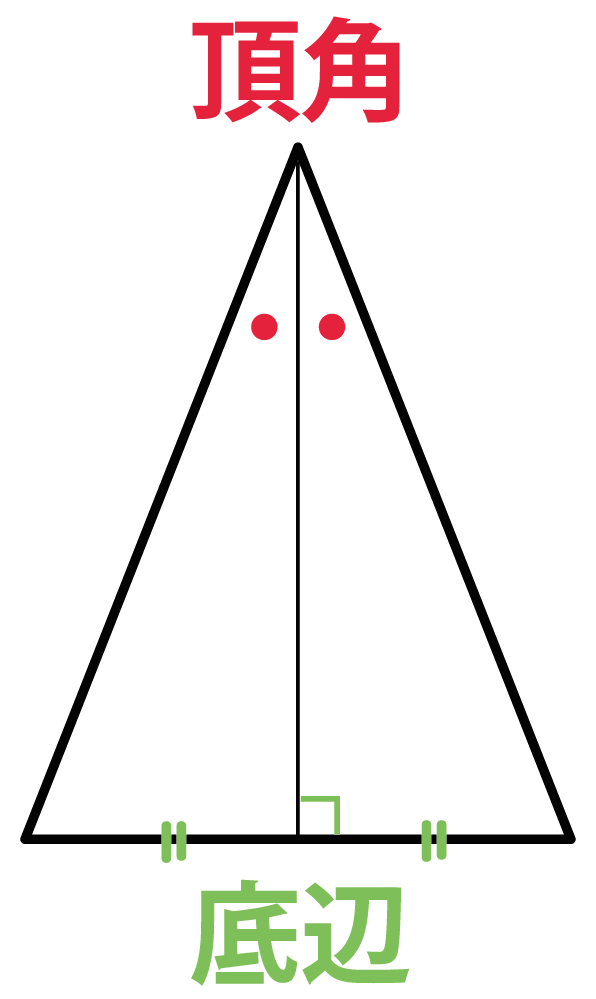
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 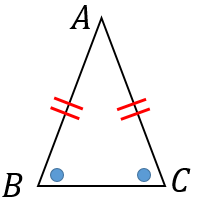 Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp | Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp | 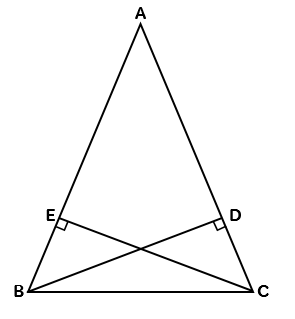 Ed City Daito Osaka Jp |  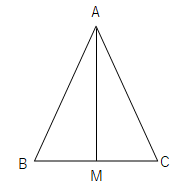Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |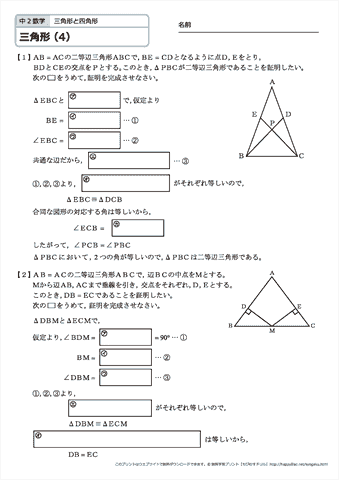
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp | 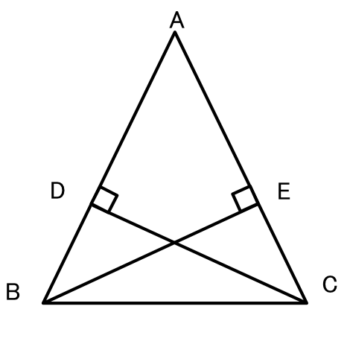 Ed City Daito Osaka Jp |
 Ed City Daito Osaka Jp |  Ed City Daito Osaka Jp |
平行線，角の二等分線，二等辺三角形の関係を用いた証明問題の作成について 永井千尋(南山大学大学院理工学研究科) 佐々木克巳(南山大学理工学部) email sasaki@nanzanuacjp 概要 本稿は，平行線，角の二等分線，二等辺三角形の関係に注目し，それを用いた証 まとめ：二等辺三角形の定理の証明は合同の性質から！ 二等辺三角形の定理は便利。 ぜんぶ、 合同な三角形の性質からきているんだ。 暗記するのも大事だけど、 なぜ、二等辺三角形の定理がつかえるのか？？ ということを知っておいてね^^ そんじゃねー Ken
Incoming Term: 二等辺三角形の証明, 二等辺三角形の証明問題, 二等辺三角形の証明の解き方, 二等辺三角形の証明方法,
0 件のコメント:
コメントを投稿